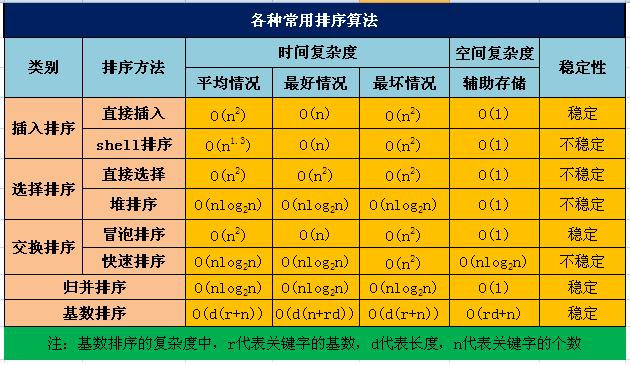
数据结构排序总结

发表于 | 分类于

数据结构排序总结

vtable

怎么记忆稳定性：

总过四大类排序：插入、选择、交换、归并（基数排序暂且不算）

比较高级一点的（时间复杂度低一点得）shell排序，堆排序，快速排序（除了归并排序）都是不稳定的，在加上低一级的选择排序是不稳定的。

比较低级一点的（时间复杂度高一点的）插入排序，冒泡排序，归并排序，基数排序都是稳定的。

（4种不稳定，4种稳定）。

怎么记忆初始序列是否对元素的比较次数有关：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/** 
  * @brief 严版数据结构书代码 
  *        最好的情况,数组本身有序，就只需执行n-1次比较，此时时间复杂度为O(n); 
  *        最坏的情况，数组本身逆序，要执行n(n-1)/2次，此时时间复杂度为O(n^2); 
  */  
void _insertSort(int R[], int n)  
{  
    int i, j, temp;  
    for ( i = 1; i < n; ++i ) {  
        if ( R[i] < R[i - 1] ) {//将R[i]插入有序字表  
            temp = R[i];        //设置哨兵  
            for ( j = i - 1; R[j] > temp; --j ) {  
                R[j+1] = R[j];  
            }  
            R[j+1] = temp;  
        }  
    }  
}

对于直接插入排序:

当最好的情况，如果原来本身就是有序的，比较次数为n-1次（分析（while (j >= 0 && temp < R[j])）这条语句）,时间复杂度为O(n)。

当最坏的情况，原来为逆序，比较次数为2+3+…+n=(n+2)(n-1)/2次，而记录的移动次数为i+1(i=1,2…n)=(n+4)(n-1)/2次。

如果序列是随机的，根据概率相同的原则，平均比较和移动的次数为n^2/4.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/** 
  * @brief 严版数据结构 选择排序 
  *        采用"选择排序"对长度为n的数组进行排序,时间复杂度最好，最坏都是O(n^2) 
  *        当最好的时候，交换次数为0次，比较次数为n(n-1)/2 
  *        最差的时候，也就初始降序时，交换次数为n-1次，最终的排序时间是比较与交换的次数总和， 
  *        总的时间复杂度依然为O(n^2) 
  */  
void _selectSort(int R[], int n)  
{  
    int i, j, temp, index;  
    for ( i = 0; i < n; ++i ) {  
        index = i;  
        for ( j = i + 1; j < n; ++j ) {  
            if ( R[index] > R[j] ) {  
                index = j;//index中存放关键码最小记录的下标  
            }  
        }  
        if (index != i) {  
            temp = R[i];  
            R[i] = R[index];  
            R[index] = temp;  
        }  
    }  
}

选择排序不关心表的初始次序，它的最坏情况的排序时间与其最佳情况没多少区别，其比较次数都为 n(n-1)/2，交换次数最好的时候为0，最差的时候为n-1，尽管和冒泡排序同为O(n)，但简单选择排序性能上要优于冒泡排序。但选择排序可以 非常有效的移动元素。因此对次序近乎正确的表，选择排序可能比插入排序慢很多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/** 
  * @brief     改进的冒泡排序 
  * @attention 时间复杂度，最好的情况，要排序的表本身有序，比较次数n-1,没有数据交换,时间复杂度O(n)。 
  *            最坏的情况，要排序的表本身逆序，需要比较n(n-1)/2次，并做等数量级的记录移动，总时间复杂度为O(n^2). 
  */  
void bubbleSort2(int R[], int n)  
{  
    int i, j, temp;  
    bool flag = TRUE;   //flag用来作为标记  
  
    for ( i = 0; i < n && flag; ++i ) {  
        flag = FALSE;  
        for ( j = n - 1; j > i; --j ) {  
            if (R[j] < R[j - 1]) {  
                temp = R[j];  
                R[j] = R[j - 1];  
                R[j - 1] = temp;  
                flag = TRUE;//如果有数据交换，则flag为true  
            }  
        }  
    }  
}

冒泡排序：
最好的情况，n-1次比较，移动次数为0，时间复杂度为O(n)。

最坏的情况，n(n-1)/2次比较，等数量级的移动，时间复杂度为O(O^2)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/** 
  * @brief 希尔排序, 对于长度为n的数组,经过 "希尔排序" 输出 
  */  
void shellSort(int R[], int n)  
{  
    int i, j, temp;  
    int k = n / 2;  
    while (k >= 1) {  
        for (i = k; i < n; ++i) {  
            temp = R[i];  
            j = i - k;  
            while (R[j] < temp && j >= 0) {  
                R[j+k] = R[j];  
                j = j - k;  
            }  
            R[j+k] = temp;  
        }  
        k = k / 2;  
    }

希尔排序初始序列对元素的比较次数有关。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/** 
  * @brief     构建 大顶堆 
  * @attention 个人版本，堆排序 
  */  
void heapAdjust(int R[], int start, int end)  
{  
    int j, temp;  
    temp = R[start];  
    for ( j = 2 * start + 1; j <= end; j = j * 2 + 1 ) {  
          
        if ( j < end && R[j] < R[j + 1] ) {  
            ++j;  
        }  
        if ( temp >  R[j] ) {  
            break;  
        }  
        R[start] = R[j];  
        start = j;  
    }  
    R[start] = temp;  
}  
  
/** 
  * @brief 堆排序 
  * @param R为待排序的数组，size为数组的长度 
  *  时间复杂度:构建大(小)顶堆，完全二叉树的高度为log(n+1)，因此对每个结点调整的时间复杂度为O(logn) 
  *           两个循环，第一个循环做的操作次数为n/2，第二个操作次数为(n-1)，因此时间复杂度为O(nlogn) 
  */  
void heapSort(int R[], int size)  
{  
    int i, temp;  
    for ( i = size / 2 - 1; i >= 0; --i ) {  
        heapAdjust(R, i, size);  
    }  
    for ( i = size - 1; i >= 0; --i ) {  
        temp = R[i];  
        R[i] = R[0];  
        R[0] = temp;//表尾和表首的元素交换  
        heapAdjust(R, 0, i - 1);
        //把表首的元素换成表尾的元素后，重新构成大顶堆，因为除表首的元素外
        //后面的结点都满足大顶堆的条件，故heapAdjust()的第二个参数只需为0  
    }  
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/** 
  * @brief 将有序的长度为n的数组a[]和长度为m的b[]归并为有序的数组c[] 
  *        只要从比较二个数列的第一个数，谁小就先取谁，取了之后在对应的数列中删除这个数。 
  *        然后再进行比较，如果有数列为空，那直接将另一个数列的数据依次取出即可。 
  *        将两个有序序列a[first...mid]和a[mid...last]合并 
  */  
void mergeArray(int a[], int first, int mid, int last, int tmp[])  
{  
    int i = first, j = mid + 1;  
    int k = 0;  
    while ( i <= mid && j <= last ) {  
        if ( a[i] <= a[j] )  
            tmp[k++] = a[i++];  
        else  
            tmp[k++] = a[j++];  
    }  
    while ( i <= mid ) {  
        tmp[k++] = a[i++];  
    }  
    while ( j <= last ) {  
        tmp[k++] = a[j++];  
    }  
    for (i = 0; i < k; i++) {//这里千万不能丢了这个  
        a[first + i] = tmp[i];  
    }  
}  
/** 
  * @brief 归并排序，其的基本思路就是将数组分成二组A，B，如果这二组组内的数据都是有序的， 
  *        那么就可以很方便的将这二组数据进行排序。如何让这二组组内数据有序了？ 
 
  *        可以将A，B组各自再分成二组。依次类推，当分出来的小组只有一个数据时， 
  *        可以认为这个小组组内已经达到了有序，然后再合并相邻的二个小组就可以了。这样通过先 (递归) 的分解数列， 
  *        再 (合并) 数列就完成了归并排序。 
  */  
void mergeSort(int a[], int first, int last, int tmp[])  
{  
    int mid;  
    if ( first < last ) {  
        mid = ( first + last ) / 2;  
        mergeSort(a, first, mid, tmp);  //左边有序  
        mergeSort(a, mid + 1, last, tmp);   //右边有序  
        mergeArray(a, first, mid, last, tmp);  
    }  
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**  
  * @brief 虽然快速排序称为分治法，但分治法这三个字显然无法很好的概括快速排序的全部步骤。 
  *        因此我的对快速排序作了进一步的说明：挖坑填数+分治法： 
  * @param R为待排数组，low和high为无序区 
  *        时间复杂度：最好O(nlogn),最坏O(n^2)，平均O(nlogn)，空间复杂度O(logn)； 
  */  
void quickSort(int R[], int low, int high)  
{  
    if ( low < high ) {  
        int i = low, j = high, temp = R[low];  
  
        while ( i < j ) {  
            //从右往左扫描，如果数组元素大于temp，则继续，直至找到第一个小于temp的元素  
            while ( i < j && R[j] >= temp ) {  
                --j;  
            }  
            if ( i < j ) {  
                R[i++] = R[j];  
            }  
            while ( i < j && R[i] <= temp ) {  
                ++i;  
            }  
            if ( i < j ) {  
                R[j--] = R[i];  
            }  
        }  
        R[i] = temp;  
        quickSort(R, low, i - 1);  
        quickSort(R, i + 1, high);  
    }  
}

各排序算法整体分析

冒泡排序、插入排序、希尔排序以及快速排序对数据的有序性比较敏感，尤其是冒泡排序和插入排序；

选择排序不关心表的初始次序，它的最坏情况的排序时间与其最佳情况没多少区别，其比较次数为 n(n-1)/2，但选择排序可以 非常有效的移动元素。因此对次序近乎正确的表，选择排序可能比插入排序慢很多。

冒泡排序在最优情况下只需要经过n-1次比较即可得出结果（即对于完全正序的表），最坏情况下也要进行n(n-1)/2 次比较，与选择排序的比较次数相同，但数据交换的次数要多余选择排序，因为选择排序的数据交换次数顶多为 n-1，而冒泡排序最坏情况下的数据交换n(n-1)/2 。冒泡排序不一定要进行 趟，但由于它的记录移动次数较多，所以它的平均时间性能比插入排序要差一些。

插入排序在最好的情况下有最少的比较次数 ，但是它在元素移动方面效率非常低下，因为它只与毗邻的元素进行比较，效率比较低。

希尔排序实际上是预处理阶段优化后的插入排序，一般而言，在 比较大时，希尔排序要明显优于插入排序。

快速排序采用的“大事化小，小事化了”的思想，用递归的方法，将原问题分解成若干规模较小但与原问题相似的子问题进行求解。快速算法的平均时间复杂度为O(nlogn) ，平均而言，快速排序是基于关键字比较的内部排序算法中速度最快者；但是由于快速排序采用的是递归的方法，因此当序列的长度比较大时，对系统栈占用会比较多。快速算法尤其适用于随机序列的排序。

因此，平均而言，对于一般的随机序列顺序表而言，上述几种排序算法性能从低到高的顺序大致为：冒泡排序、插入排序、选择排序、希尔排序、快速排序。但这个优劣顺序不是绝对的，在不同的情况下，甚至可能出现完全的性能逆转。

对于序列初始状态基本有正序，可选择对有序性较敏感的如插入排序、冒泡排序、选择排序等方法

对于序列长度 比较大的随机序列，应选择平均时间复杂度较小的快速排序方法。

各种排序算法都有各自的优缺点，适应于不同的应用环境，因此在选择一种排序算法解决实际问题之前，应当先分析实际问题的类型，再结合各算法的特点，选择一种合适的算法

这里特别介绍下快速排序：

快速排序的时间主要耗费在划分操作上，对长度为k的区间进行划分，需要k-1次关键字比较。

（1）最坏的时间复杂度

最坏情况是每次划分选取的基准都是当前无序区中关键字最小（或最大）的记录，划分的结果是基准左边的子区间为空（或右边的子区间为空），而划分所得的另一个非空的子区间中记录数目，仅仅比划分前的的无序区中记录个数减少一个。

因此，快速排序必须做n-1次划分，第i次划分开始区间长度为n-i+1,所需的比较次数为n-i(1<=i<=n-1),故总的比较次数达到最大值：n(n-1)/2；

如果按上面给出的划分算法，每次取当前无序区的第1个记录为基准，那么当文件的记录已按递增序(或递减序)排列时，每次划分所取的基准就是当前无序区中关键字最小(或最大)的记录，则快速排序所需的比较次数反而最多。

（2）最坏的时间复杂度

在最好情况下，每次划分所取的基准都是当前无序区的”中值”记录，划分的结果是基准的左、右两个无序子区间的长度大致相等。总的关键字比较次数：
0(nlgn)

（3）平均时间复杂度

尽管快速排序的最坏时间为O(n2)，但就平均性能而言，它是基于关键字比较的内部排序算法中速度最快者，快速排序亦因此而得名。它的平均时间复杂度为O(nlgn)。

（4）空间复杂度

快速排序在系统内部需要一个栈来实现递归。若每次划分较为均匀，则其递归树的高度为O(lgn)，故递归后需栈空间为O(lgn)。最坏情况下，递归树的高度为O(n)，所需的栈空间为O(n)。